Physikalische Experimente
– Einführung in naturwissenschaftliche Arbeitsweisen –
Liegen die Messpunkte nicht entlang einer Ursprungsgeraden, so stellt man zunächst eine Vermutung über den mathematischen Zusammenhang der Messgrößen auf. Diese sogenannte Proportionalitätsvermutung (Hypothese) findet man, indem man eine mathematische Funktion sucht, deren Graph der Ausgleichskurve ähnelt.
Um die Vermutung anschließend zu überprüfen, berechnet man aus den Werten der veränderlichen Messgröße mithilfe der gefundenen mathematischen Funktion neue Werte und zeichnet aus diesen Werten ein weiteres Diagramm.
Liegen die Messpunkte jetzt entlang einer Ausgleichgeraden hat man die Messwerte linearisiert und den richtigen Zusammenhang ermittelt und kann anschließend weiter verfahren, wie im Kapitel «Lineare Zusammenhänge» beschrieben.
Eine Zusammenfassung des hier beschriebenen Verfahrens sowie die Graphen häufig vorkommender mathematischer Funktionen finden sich auf der Abbildung rechts (anklicken zum Vergrößern)
Beispiel:
Die Ausgangshöhe einer Kugel und ihre Geschwindigkeit am Fuße einer schiefen Ebene werden gemessen (Spalten 1 und 2).
Die Messwerten werden in ein Diagramm eingetragen.
Die Ausgleichskurve entlang der Messpunkte ähnelt dem Graphen einer Wurzelfunktion. Daraus ergibt sich die Hypothese (Vermutung):
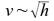
Zur Überprüfung der Hypothese werden zunächst aus den Messwerten h die neuen Werte
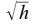
berechnet (Spalte 3 in der Tabelle oben) und anschließend in ein weiteres Diagramm eingetragen.
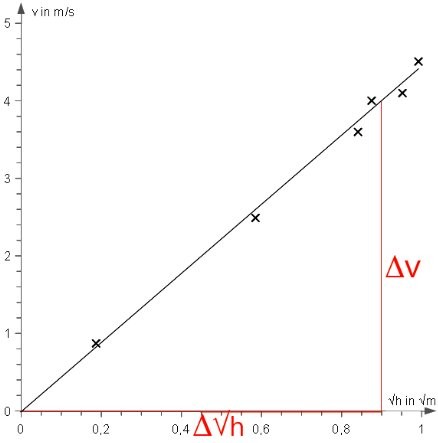
Die Ausgleichskurve entlang der eingetragenen Punkte ergibt eine Ursprungsgerade.
Die Hypothese
bestätigt sich. Für die Ausgleichsgerade ergibt sich die Gleichung:
Mithilfe des Steigungsdreiecks wird der Proportionalitätsfaktor bestimmt:
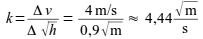
Die Formel, mit der man die Geschwindigkeit auf der Schiefen Ebene berechnen kann, lautet also:
Übungsaufgabe:
Ermitteln Sie eine Formel zur Berechnung des Schalldrucks p im Abstand r von einer Schallquelle sowie Zahlenwert und Einheit des Proportionalitätsfaktors nach dem oben gezeigten Verfahren (Messwerte siehe Tabelle rechts).
