Liegen die Messpunkte auf (oder nahe bei) einer Ursprungsgeraden (sog. Ausgleichsgerade), so besteht ein linearer Zusammenhang zwischen den Messwerten. Der
Abstand von der Geraden sollte dabei für alle Messpunkte etwa gleich groß sein.
Die Messgrößen sind proportional zueinander (»verhältnisgleich«). Schreibweise:
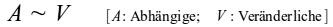
Die Gerade erfüllt die allgemeine Geradengleichung:

k: Konstante, Proportionalitätsfaktor;
math. Formulierung: y = m·x [+b]
der y-Achsenabschnitt [+b] entfällt bei Ursprungsgeraden
Zeichnen Sie ein Steigungsdreieck an die Ausgleichsgerade Ihres Diagramms und bestimmen Sie Wert und Einheit von k nach folgender Formel:

∆A, ∆V: Höhe, Breite des Steigungsdreiecks

Beispiel:
Die Massen m für verschiedene Volumina V eines Stoffes werden gemessen.
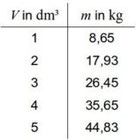
Die Messwerten trägt man in ein Diagramm ein.

Die Messpunkte liegen entlang einer Ausgleichsgeraden (einzeichnen), daher gilt der Zusammenhang: m~V
Für die Ausgleichsgerade ergibt sich die Gleichung: m = k·V
Mithilfe des Steigungsdreiecks (ebenfalls einzeichnen) bestimmt man den Proportionalitätsfaktor k:

Die Formel, mit der man die Masse eines gegebenen Volumens dieses Stoffes berechnen kann, lautet also:

 Physikalische Experimente
– Einführung in naturwissenschaftliche Arbeitsweisen –
Physikalische Experimente
– Einführung in naturwissenschaftliche Arbeitsweisen –

