Genauigkeit
In der Physik werden Werte verwendet, die vorher gemessen wurden, auch wenn dies nicht immer ausdrücklich erwähnt wird. Manchmal werden auch berechnete Werte verwendet, deren Ausgangswerte aber ebenfalls zuvor gemessen wurden. Da solche Messwerte niemals hundertprozentig exakt sein können (siehe «Messfehler»), haben alle Zahlenwerte eine sogenannte Genauigkeit (egal ob Mess- oder Rechenwert). Diese Genauigkeit kann aus der Darstellung des Zahlenwertes einer physikalischen Größe abgelesen werden (Anzahl der Ziffern und Position des Kommas). Sie beträgt die Hälfte des Wertes der kleinsten Stelle, auf die gerundet wurde.
- Beispiel 1: Bei der Messung einer Strecke erhält man als Ergebnis s=1,234 km. Der Wert der kleinsten Stelle (hier die Ziffer 4) beträgt 0,001 km oder 1 m und die Genauigkeit der Streckenmessung somit ±½ m, d.h. der tatsächliche Wert liegt zwischen s=1,2335 km und s=1,2344 km (runden auf 3 Nachkommastellen ergibt bei diesen Zahlenwerten jeweils 1,234).
-
Beispiel 2: Bei der Messung einer anderen Strecke erhält man als Ergebnis
s=12,345 m. Der Wert der kleinsten Stelle (hier die Ziffer 5) beträgt 0,001 m oder
1 mm und die Genauigkeit der Streckenmessung somit ±½ mm, d.h. der tatsächliche Wert liegt zwischen s=12,3445 m und s=12,3454 m (runden auf 3 Nachkommastellen ergibt bei diesen Zahlenwerten jeweils 12,345).
Anzahl der Stellen
Das Ergebnis einer Rechnung oder Messung sollte zwischen 1 und 9999 liegen, größere oder kleinere Werte werden unter Verwendung von Zehnerpotenzen bzw. Einheitenvorsätzen angegeben.
Der Zahlenwert sollte nicht mehr als 4-5 Stellen aufweisen, alle Stellen vor und nach dem Dezimalkomma zusammengenommen. Zahlenwerte mit mehr Stellen werden entsprechend gerundet:
- Beispiel 1: Bei der Messung einer Strecke erhält man als Ergebnis s=1.234.567 m. Mithilfe von Zehnerpotenzen und auf 5 Stellen gerundet gibt man die gleiche Strecke als

- Beispiel 2: Bei der Messung einer anderen Strecke erhält man als Ergebnis s=0,001234567 m. Mithilfe von Zehnerpotenzen und auf 5 Stellen gerundet gibt man die gleiche Strecke als

Werte mit Nullen
Bei Zahlenwerten mit endenden Nullen ist eine Aussage über die Genauigkeit schwieriger. Der Zahlenwert in den drei folgenden Beispielen beträgt immer s = 20 km:
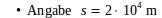
→ Wert der kleinsten Stelle 10 km → Genauigkeit ±5 km,
d.h. tatsächlicher Wert s = {15 … 24} km

→ Wert der kleinsten Stelle 1 km → Genauigkeit ± ½ km,
d.h tatsächlicher Wert s = {19,5 … 20,4} km
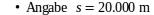
→ Wert der kleinsten Stelle 1 m → Genauigkeit ± ½ m,
d.h tatsächlicher Wert s = {19,9995 … 20,0004} km
Rechenergebnisse
Ein Zahlenwert als Ergebnisse einer Berechnung kann natürlich nicht genauer sein, als die Zahlenwerte, die für diese Berechnung verwendet wurden. In dem folgenden Beispiel wird aus einer Strecke mit einer Genauigkeit von ± 0,5 m und einer Zeit mit einer Genauigkeit von ± 0,05 s (das ist jeweils ½ des Wertes der kleinsten Stelle) die Geschwindigkeit berechnet:
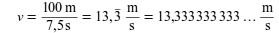
(Das Ergebnis hat unendlich viele Stellen)
Die Genauigkeit der berechneten Geschwindigkeit geht also weit über die Genauigkeit der gemessenen Strecken- und Zeitwerte hinaus. Die Rechnung ist zwar mathematisch korrekt, wegen der gestiegenen Genauigkeit jedoch physikalisch nicht sinnvoll. Ergebnisse aus Rechnungen sollten daher maximal eine Stelle mehr haben, als die Zahl mit den wenigsten Stellen:

(Das Ergebnis hat 2 + 1 = 3 Stellen)
Zusammenfassung
Endergebnis werden also sinnvoll, Zwischenergebnisse dagegen nicht gerundet. Gestalten Sie den Rechenweg nach Möglichkeit so, dass keine Zwischenergebnisse notwendig sind. Falls doch, runden Sie geschriebene Zwischenergebnisse auf eine sinnvolle Stellenanzahl, verwenden Sie für den weiteren Rechenweg aber bitte das Zwischenergebnis aus dem Taschenrechnerspeicher (mit der vollen Stellenanzahl).
Übungsaufgaben:
- Sie bestimmen Fallzeiten für verschiedene Gegenstände, die Ihr Bekannter aus dem Fenster im Stockwerk über Ihnen wirft. Gleichzeitig ruft er laut „los“, während
Sie Ihre Stoppuhr starten. Sobald der Gegenstand an Ihrem Fenster vorbeikommt, stoppen Sie die Uhr. Um die Genauigkeit der Messung zu erhöhen, schlägt Ihr Bekannter vor, eine Stoppuhr zu
benutzen, die auf 1/1000 s genau messen kann. Bewerten Sie diesen Vorschlag. Was können Sie noch tun, um die Genauigkeit der Messung zu erhöhen?
- Geben Sie für die folgenden 3 Beispiele (a-c) die Genauigkeit bzw. den Messfehler an:
a) Auf einem Gliedermaßstab (»Zollstock«) lesen Sie 0,024 Meter ab.
b) Mit dem Tageskilometerzähler in einem Auto bestimmen Sie als Länge Ihres Weges zur Schule 25,3 Kilometer.
c) Mit dem Sekundenzeiger einer Uhr messen Sie die Dauer einer Pendelschwingung mit 3 Sekunden.
 Physikalische Experimente
– Einführung in naturwissenschaftliche Arbeitsweisen –
Physikalische Experimente
– Einführung in naturwissenschaftliche Arbeitsweisen –

