+ + + B e i s p i e l z u r O r i e n t i e r u n g + + +
Am Beispiel dieses Experiments soll verdeutlicht werden, wie die
Vorbereitung, das Protokoll sowie das Thesenpapier aufgebaut sind.
P R O T O K O L L
Name/Klasse/Datum/
- Namen aller am Experiment beteiligten Schüler
- Klassenbezeichnung
- Datum der Ausfertigung (bei verschiedenen Versionen das jeweils aktuelle)
Thema
Schwingung einer Saite
Ziel des Versuchs
Untersucht werden soll der Zusammenhang zwischen der Frequenz der Grundschwingung einer beidseitig eingespannten Saite, ihrer Länge und ihrer Belastung mit verschiedenen Zugmassen.
Funktion der Messgeräte
Bei dem im Versuch verwendeten Oszilloskop erzeugen Elektronen beim Auftreffen auf den Bildschirm einer Kathodenstrahlröhre einen leuchtenden Punkt. Dieser Elektronenstrahl kann durch elektrische
Felder vertikal und horizontal abgelenkt werden. Die horizontale Ablenkung erfolgt durch eine im Oszilloskop erzeugte Wechselspannung, die bewirkt, dass der Lichtpunkt vom linken zum rechten Rand
wandert und danach wieder nach links zurückspringt. Bei genügend großer Geschwindigkeit nimmt man den wandernde Punkt als horizontaler Strich.
Die gemessene Spannung wird dem Oszilloskop von außen zugeführt und sorgt für die vertikale Ablenkung des Lichtpunktes. Auf dem Leuchtschirm wird also der zeitliche Verlauf der gemessenen
Spannung dargestellt.
Messgrößen (direkte und indirekte)
l: Saitenlänge, Abstand zwischen Halter und Steg
m: Zugmasse, Gesamtmasse der angehängten Massestücke
T: Schwingungsdauer, Dauer einer Schwingung der Saite
F = m · g: Gewichtskraft, die auf die angehängte Gesamtmasse wirkt; entspricht der Zugkraft auf die Saite
f = T ˉ¹: Frequenz der Saitenschwingung
Beschreibung des Versuchsaufbaus (mit Skizze)

Ein Ende eines Fadens – zur Verfügung stehen drei unterschiedliche Materialien (Garn, Nylon, Paketschnur) – wird an einem horizontal verschiebbaren Halter befestigt. Das andere Ende des Faden wird über den Steg eines Resonanzkastens und eine Umlenkrolle nach unten geführt. An dieses Fadenende werden während des Experiments verschieden schwere Zugmassen angehängt.
Parallel zum Faden wird ausgehend vom Steg des Resonanzkastens ein Maßstab befestigt. Auf dem Maßstab ist ein verschiebbarer Reiter angebracht. Mit diesem wird der Abstand zwischen Halter und Steg und damit die Saitenlänge bestimmt.
Vor der Schallöffnung des Resonanzkastens wird ein Mikrofon positioniert, das an einem Oszilloskop angeschlossen wird.
Beschreibung der Versuchsdurchführung
1. Messreihe: Der Halter, an dem das eine Fadenende befestigt ist, wird an einer Stelle festgeschraubt. Mit dem Reiter auf dem Maßstab wird die Position des Halters und damit die Saitenlänge abgelesen und notiert. Am anderen, unteren Fadenende wird eine (mittlere) Zugmasse befestigt und deren Wert notiert. Nun wird der Faden etwa in der Mitte zwischen Halter und Steg angezupft. Mithilfe des Oszilloskops wird die Frequenz bestimmt und notiert (siehe Auswertung).
Nun wiederholt man die Messung mit den anderen Saitenmaterialien bei gleicher Saitenlänge und Zugmasse. Danach verschiebt man den Halter an eine andere Position, liest mithilfe des Reiters die neue Saitenlänge ab, bestimmt die Frequenz der schwingenden Saite und notiert beide Werte, bevor man diesen Vorgang mit den anderen Saitenmaterialien ebenfalls wiederholt. Am Ende liegt zu jedem Saitenmaterial eine Messreihe mit fünf verschiedenen Wertepaaren {Saitenlänge; Frequenz} vor.
2. Messreihe: Der Halter wird wieder an einer Position befestigt, die Saitenlänge wird abgelesen und notiert. Wieder hängt man eine Zugmasse an das untere Fadenende, notiert auch deren Wert, zupft die Saite wieder zwischen Steg und Halter an und bestimmt und notiert die Frequenz mithilfe des Oszilloskops (siehe Auswertung).
Jetzt wird die Zugmasse am unteren Fadenende verändert und der Faden wieder zwischen Halter und Steg angezupft. Die Werte für Masse und Frequenz werden notiert, und die Zugmasse abermals variiert. Anschließend wiederholt man die Messreihe, wobei die anderen Fadenmaterialien verwendet werden. Am Ende liegt zu jedem Fadenmaterial eine Messreihe mit fünf verschiedenen Wertepaaren {Zugmasse; Frequenz} vor.
Beschreibung der Beobachtung
Während des Versuchs zeigt sich, dass bei einer Verkürzung der Saitenlänge oder einer Vergrößerung der Zugmasse die Tonhöhe zunimmt. Eine genauere Betrachtung der Messwerte (siehe unten) liefert folgende Ergebnisse:
1. Messreihe: Bei Verdoppelung der Saitenlänge halbiert sich die Frequenz etwa.
2. Messreihe: Bei Vervierfachung der Zugmasse verdoppelt sich die Frequenz etwa.
Messprotokolle

Auswertung

Interpretation des Schirmbildes
Auf dem Schirm des Oszilloskops sieht man den zeitlichen Verlauf der vom Mikrofon aufgenommenen Schwingungen der Saite. Dabei nimmt die Amplitude der Schwingung kontinuierlich ab, der Ton wir leiser.
Während der Belichtungszeit des Fotos (0,2s) wurden auf dem Bildschirm des Oszilloskops etwa 20 Kurven mit abnehmender Amplitude gezeichnet (ein Bildschirmdurchlauf benötigt 10ms). Das führt zu den vielen überlagerten Kurven auf dem Schirm.
Bestimmung der Frequenz
Aus dem Schirmbild ermittelt man zunächst die Schwingungsdauer (hier: 7,6 x-Einheiten für 3 Schwingungen, 1 Einheit ≙ 1ms) und bestimmt daraus dann die Frequenz:

Zeichnen der Diagramme f=f(l) und f=f(F) und aufstellen der Hypothesen

1. Messreihe
Zunächst wird die Zugkraft (Gewichtskraft) F=m·g der konstant gehaltenen Zugmasse m berechnet und oberhalb der Tabelle notiert.
Danach werden Frequenz f und Saitenlänge l für verschiedene Saitenmaterialien in ein gemeinsames Diagramm eingetragen und jeweils mit einer passenden Ausgleichskurve ergänzt (Abbildung rechts).
Aufgrund der Ähnlichkeit der Graphen zu einer Hyperbel ergibt sich folgende Hypothese:


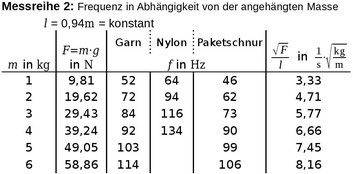
2. Messreihe
Zunächst wird aus den Messwerten aller angehängter Massen m über F=m·g jeweils die Zugkraft F berechnet und in der Tabelle notiert (2. Spalte). Dann werden Frequenz f und Zugkraft F für verschiedene Saitenmaterialien in ein gemeinsames Diagramm eingetragen und mit einer passenden Ausgleichskurve ergänzt (Abbildung rechts).
Aufgrund der Ähnlichkeit der Graphen zu einer Wurzelfunktion ergibt sich folgende Hypothese:

Zusammenführen der Zusammenhänge in die neue Größe √F/l
Ist eine Größe A proportional zu einer Größe B und unabhängig davon auch proportional zu einer anderen Größe C, so ist A auch proportional zum Produkt B·C.
Für Frequenz f, Saitenlänge l und Zugkraft F bedeutet das folgendes:
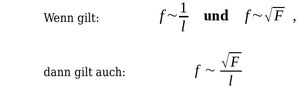
Zur Überprüfung dieser neue Hypothese werden zunächst die Messwerte linearisiert, indem aus den Werten F und l eine neue Größe √F/l berechnet, und anschließend zusammen mit der Frequenz f in ein gemeinsames Diagramm eingetragen wird.
Zeichnen des Diagramms f=f(√F/l) und aufstellen der allgemeinen Formel

Für alle Messungen der beiden Messreihen werden aus den Werten F und l jeweils √F/l berechnet und in der jeweiligen Tabelle notiert (rechte Spalte). Danach wird aus allen Wertepaare f und √F/l ein gemeinsames Diagramm erstellt. Dabei zeigt sich, dass alle Messpunkte (aus beiden Tabellen) eines Saitenmaterials auch entlang der gleichen Ausgleichsgeraden liegen.
Damit sind die Hypothesen bestätigt worden und es gilt folgende

Proportionalitätsfaktoren
Berechnung
Hierzu bestimmt man Höhe und Breite der Steigungsdreiecke an den Graphen f=f(√F/l ). Um das Diagramm nicht zu unübersichtlich zu gestalten, wurde im Diagramm nur das Steigungsdreieck für den Graph «Paketschnur» eingezeichnet.

Erläuterung
Der Wert des Proportionalitätsfaktors ist bei Paketschnur am niedrigsten, bei Garn etwa 15% höher und bei Nylon etwa dreimal so hoch. Die Frequenzen, die man mit den drei Materialien bei gleicher Länge und Spannung erzeugen kann stehen genau in der gleichen Reihenfolge. Gleichzeitig ist die Paketschnur auch das Material mit dem größten Werten für Durchmesser und Masse, Nylon das mit den niedrigsten.
Je größer die Masse einer Saite, desto langsamer die Schwingung und desto niedriger die Frequenz. Da sich die schwingende Masse der Saite aber mit der Länge ändert, ist der Proportionalitätsfaktor von Länge (und damit Masse) unabhängig, nämlich konstant. Gleichwohl wird die Frequenz davon bestimmt, ob Paketschur, Garn oder Nylon schwingt. Als eine weitere Materialkonstante mit Einfluss auf die Schwingung kommt die Dichte in Betracht. Dieser Zusammenhang soll im nächsten Abschnitt untersucht werden.
Prozentuale Abweichung
Die prozentuale Abweichung (p.A.) gibt die Abweichung zwischen Messwert (Ist-Wert) und erwartetem Wert (Soll-Wert) an. Mit ihrer Hilfe kann die Qualität einer Messung beurteilt werden. In diesem Fall sollen die experimentell ermittelten Proportionalitätsfaktoren mit ihren Soll-Werten verglichen werden.
Ermittlung der Sollwerte
In der Literatur findet man eine Formel zur Berechnung der Frequenz einer schwingenden Saite. Vergleicht man diese mit der allgemeinen Formel aus dem Versuch, ergibt sich eine Formel, mit der der Proportionalitätsfaktor aus den Kenngrößen des Saitenmaterials berechnet werden kann (Soll-Wert):

Darin bedeuten: Dichte (ϱ) des Saitenmaterials; Querschnittsfläche (A); Volumen (V*) und Masse (m*) bezogen auf ein Teilstück der Länge (l*) der gespannten Saite (zur Unterscheidung von Zugmasse und Seitenlänge hier mit einem Stern gekennzeichnet)
Zur Messung der benötigten Größen wird zunächst die Länge l* eines Teilstücks der gespannten Saite (Zugmasse 2kg) markiert und gemessen. Anschließend wird die Saite entspannt, das markierte Teilstück herausgetrennt und seine Masse m* gewogen.
Achtung: Damit die Proportionalitätsfaktoren (Soll- und Ist-Wert) miteinander vergleichbar sind, müssen sie unter vergleichbaren Bedingungen ermittelt werden, also mit vergleichbarer Saitenspannung.
Berechnung der prozentualen Abweichung
Aus den für jedes Saitenmaterial gemessenen Werte (l*, m*) werden die erwarteten Proportionalitätsfaktoren (Soll-Werte) berechnet. Aus diesen Soll-Weten wird mit den Ist-Werten (Abschnitt «Proportionalitätsfaktoren», siehe oben) die prozentuale Abweichung (p.A.) berechnet (Messwerte, Ergebnisse, Formeln in der Tabelle).

Angabe der Messfehler
Bestimmung der Zugkraft
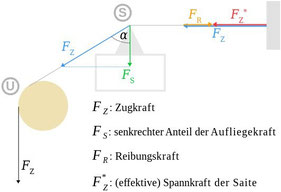
Die Zugkraft ist im reibungsfrei geführten Abschnitt der Saite an allen Stellen gleich groß und entspricht der Gewichtskraft der Zugmasse.
Aufgrund des abgewinkelten Verlaufs am Steg S drückt die Saite hier mit einer Kraft (grün) senkrecht nach unten. Dies bewirkt eine Reibungskraft (orange), die die Zugkraft zwischen Steg und Halter herabsetzt, sodass die effektive Spannkraft der Saite (rot) hier geringer ausfällt.
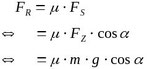
Zur Berechnung der (Haft-)Reibungskraft benötigt man den Haftreibungskoeffizienten µ (auch Haftreibungszahl) und den senkrechten Anteil der Aufliegekraft. Die erhält man aus der Zugmasse m, der Fallbeschleunigung g und dem Winkel α.
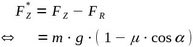
Die Kraft, mit der die Saite zwischen Halter und Steg tatsächlich gespannt wird, ergibt sich aus der Differenz zwischen Zug- und Reibungskraft.
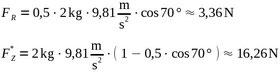
Die Haftreibungszahl µ=0,5 erhält man, indem man in einem Tabellenbuch nach der passenden Materialpaarung sucht (hier: Holz–Hanf). Die anderen Größen können direkt am Aufbau gemessen werden.

Der Fehler, der durch Reibung der Saite auf dem Steg entsteht, beträgt also etwa 17% und ist unabhängig von der Zugmasse.
Man kann diesen hohen Fehler allerdings deutlich verringern, indem man vor der Frequenzmessung die Saite unmittelbar vor oder hinter dem Steg etwas anhebt und so die Reibung der Saite am Steg kurzzeitig aufhebt.
Bestimmung der Frequenz
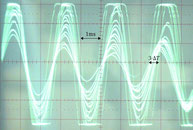
Auf dem Bildschirm des Oszilloskops werden immer mehrere Schwingungsdurchläufe überlagert abgebildet, das führt zu einigen Schwierigkeiten bei der genauen Bestimmung der Schwingungsdauer. Daher liest man zunächst die Dauer für eine möglichst hohe Anzahl von Schwingungen ab (3T im abgebildeten Beispiel) sowie den Unterschied zwischen größtem und kleinstem abzulesenden Wert (hier 3∆T). Aus diesen Werten berechnet man Schwingungsdauer (T) und Messungenauigkeit (∆T/2).
Die Frequenz f berechnet sich als Kehrwert der Schwingungsdauer T (also f=1/T). Die Messungenauigkeit der Frequenz ∆f erhält man entweder, indem man die Frequenzen der größten und kleinsten Schwingungsdauer und anschließend deren Differenz berechnet, oder indem man einfach die Messungenauigkeit der Schwingungsdauer in Prozent umrechnet. Die Prozentangabe ändert sich nicht.

Änderung des Saitenquerschnitts
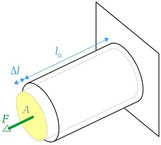
Durch Spannen wird die Saite, ausgehend von ihrer ungespannten Länge l₀ im elastischen Bereich des Materials proportional zur Zugkraft F um ∆l verlängert
(siehe Formel ➀).
Da das Volumen V der Saite konstant bleibt, verringert sich beim Spannen also ihre Querschnittsfläche A
(siehe Formel ➁).


Nach der oben angegebenen Literaturformel wird die Frequenz der Saitenschwingung auch von der Querschnittsfläche beeinflusst. Das Diagramm zeigt die Graphen von experimenteller (f(F), durchgezogen) und Literaturformel (f(F,A), gestrichelt).
Nimmt man die Querschnittsfläche als konstant an, weichen die gemessenen Werte mit steigender Zugkraft immer stärker von den erwarteten Werten ab. Der Fehler kann hierbei nur geschätzt werden, da die bestimmenden Größen (Dichte, Volumen, Elastizitätsmodul der Saite) nicht erfasst worden sind. Demnach beträgt der Fehler bei einer Zugkraft von 40N etwa -7% (die Werte dazu sind dem Diagramm entnommen).
Quellenangaben
Oszilloskop:
https://de.wikipedia.org/wiki/Oszilloskop
Impulse Physik Oberstufe, S. 114 ff., Ernst Klett Verlag, Stuttgart
Saitenschwingung:
http://www.spektrum.de/lexikon/physik/saitenschwingungen/12681
Impulse Physik Oberstufe, S. 178 ff., Ernst Klett Verlag, Stuttgart
Haftreibung:
https://de.wikipedia.org/wiki/Reibungskoeffizient
Weiter zum Thesenpapier
 Physikalische Experimente
– Einführung in naturwissenschaftliche Arbeitsweisen –
Physikalische Experimente
– Einführung in naturwissenschaftliche Arbeitsweisen –






